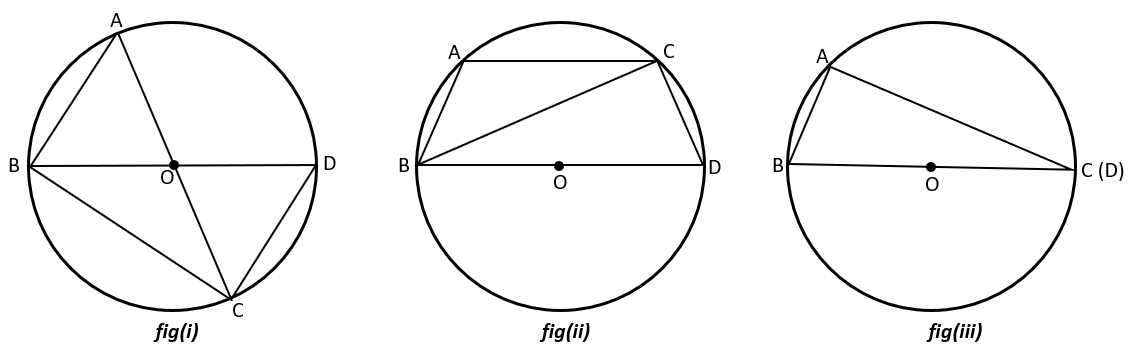
Let ABC be the triangle with all three vertex on the circumference of the circle with center O as shown in fig above.BO is drawn if the angle is either acute or obtuse as shown in fig(i) and fig(ii). Also, BO is  produced to D to form the diameter BD as shown in fig. [C coincides D in fig (iii)]Then, circum-radius=OB=R(radius of circle) and BD=2R and angle BCD=90⁰ [in fig (i) and (ii)] being angle at semi-circle. To Prove: 
1. For a triange as shown in fig(i)
    BAC=BDC                     [angle subtended by same segment]
i.e., angle A = angle D.........(i)In triangle BDC,
    

2. For a triangle as shown in fig(ii)
In triangle BDC,
    3. For a triangle as shown in fig(iii)
     BC = 2R = 2R sin A                    [A=90⁰ , sin A = sin 90⁰ = 1]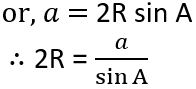

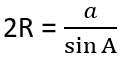
Hence, for every condition we have, Similarly, we can prove, Combining these we get,
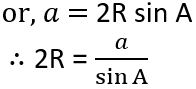
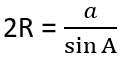
, which is the Sine Law in terms of circum-radius.