Antiderivatives
Antiderivtaives Antiderivatives are the opposite of derivatives. An antiderivative is a function that reverses what the derivative does. One function has many antiderivatives, but they al...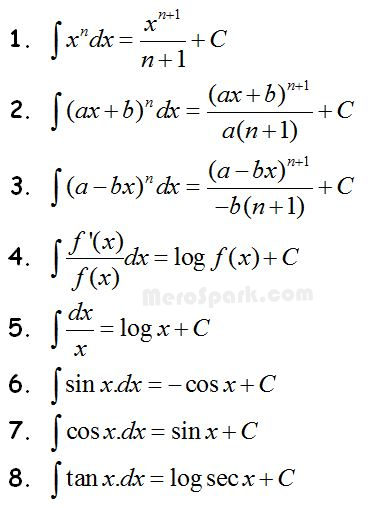

Integration of rational fraction:
In order to convert improper rational function into a proper one, we can use long division:
P(x)Q(x)=F(x)+R(x)Q(x),
where F(x) is a polynomial, R(x)Q(x) is a proper rational function.
To integrate a proper rational function, we can apply the method of partial fractions.
This method allows to turn the integral of a complicated rational function into the sum of integrals of simpler functions.
The denominators of the partial fractions can contain non-repeated linear factors, repeated linear factors, non-repeated irreducible quadratic factors, and repeated irreducible quadratic factors.
To evaluate integrals of partial fractions with linear or quadratic denominators, we use the following 6 formulas:
1.∫Adxax+b=Aln|ax+b|
2.∫Adx(ax+b)k=Aa(1−k)(ax+b)k−1
For partial fractions with irreducible quadratic denominators, we first complete the square:
ax2+bx+c=a[(x+b2a)2+4ac−b24a2].
Hence, we can write:
∫Ax+B(ax2+bx+c)kdx=∫At+B′[a(t2+m2)]kdt=1ak∫At+B′(t2+m2)kdt,
where
t=x+b2a,m2=4ac−b24a2,B′=B−Ab2a.
The possible cases for fractions with quadratic denominators are covered by the following integrals:
3.∫tdtt2+m2=12 ln(t2+m2)
4.∫dtt2+m2=1mtan-1tm
5.∫tdt(t2+m2)k=12(1−k)(t2+m2)k−1
Finally, the integral ∫dt(t2+m2)k can be evaluated in k steps using the reduction formula
6.∫dt(t2+m2)k=t2m2(k−1)(t2+m2)k−1+2k−32m2(k−1)∫dt(t2+m2)k−1