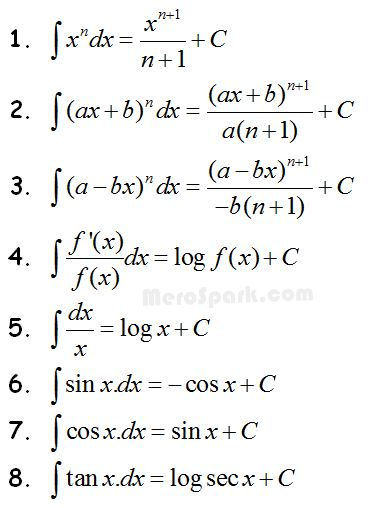
Standard integrals (I)

∫dxa2−x2=12alog(a+xa−x)∫dxa2−x2=12alog(a+xa−x) + C

∫dxx2−a2=12alog(x−aa+x)∫dxx2−a2=12alog(x−aa+x) + C

∫dxx2+a2=1atan−1xa∫dxx2+a2=1atan−1xa + C

∫dxa2−x2√=sin−1xa∫dxa2−x2=sin−1xa + C

∫dxx2−a2√=log(x+x2−a2−−−−−−√)∫dxx2−a2=log⁡(x+x2−a2)+ C

∫dxx2+a2√=log(x+x2+a2−−−−−−√)∫dxx2+a2=log⁡(x+x2+a2) + C

Standard integrals (II)

Formula for Integration by parts

 ∫ (uv) dx = u∫ vdx- ∫ (dudx)∫vdxdudx)∫vdx

∫ eax cosbxdx=eax (acosbx+bsinbx)a2+b2(acosbx+bsinbx)a2+b2

∫ eax sinbxdx=eax (asinbx−bcosbx)a2+b2

Standard integral of trigonometrical functions:

Integral of hyperbolic function:

∫sinhx dx = coshx+ c

∫ coshx dx = sinhx+ c

∫tanhx dx = ln(coshx )+ c

∫ cotdx = ln|sinhx|+ c

∫ sechx dx= tan-1 |sinhx|+c

∫ cosechx dx= ln |tanx2x2 |+c

Standard integral (III)

∫dxasinx+bcosxdxasinx+bcosx

    =1a2√+b2log(tan12(x+tan−1ba))+c