Differentials
Differentials:In calculus, the differential represents the principal part of the change in a function y = f(x) with respect to changes in the independent variable. The dif...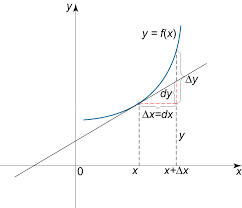

Rolle's Theorem:
If the function f(x) is
1) continuous in the closed interval [a,b]
2) differentiable in the open interval (a,b)
3) f(a)=f(b)
then there exists at least one point c belonging to (a,b) such that f '(c)=0
Rolle's theorem statement:
Mathematically, Rolle’s theorem can be stated as:
Let f : [a, b] → R be continuous on [a, b] and differentiable on (a, b), such that f(a) = f(b), where a and b are some real numbers. Then there exists some c in (a, b) such that f′(c) = 0.
Geometrical interpretation of Rolle's theorem:
In the given graph, the curve y = f(x) is continuous between x =a and x = b and at every point, within the interval, it is possible to draw a tangent and ordinates corresponding to the abscissa and are equal then there exists at least one tangent to the curve which is parallel to the x-axis.
Algebraically, this theorem tells us that if f (x) is representing a polynomial function in x and the two roots of the equation f(x) = 0 are x =a and x = b, then there exists at least one root of the equation f‘(x) = 0 lying between these values.
The converse of Rolle’s theorem is not true and it is also possible that there exists more than one value of x, for which the theorem holds good but there is a definite chance of the existence of one such value.
If any of the conditions of Rolle's theorem be not satisfied , then the conclusion of Rolle's theorem will not be true which is failure of this theorem.
Mean Value Theorem:
If a function f(x) is
1) continuous in the closed interval [a,b]
2) differential in he open interval (a,b)
then there exists atleast one value c belonging to (a,b) such that ;

This is known as Lagrange 's mean value theorem .
Geometrical Interpretation of Mean Value Theorem:
In the given graph the curve y = f(x) is continuous from x = a and x = b and differentiable within the closed interval [a,b] then according to Lagrange’s mean value theorem, for any function that is continuous on [a, b] and differentiable on (a, b) then there exists some c in the interval (a, b) such that the secant joining the endpoints of the interval [a, b] is parallel to the tangent at c.
f′(c) = f(b)–f(a)b−a