4 Maths -- Applications of Derivatives

ask mattrab Visit www.askmattrab.com for more academic resources.

Differentials

0 Questions 1616 Views

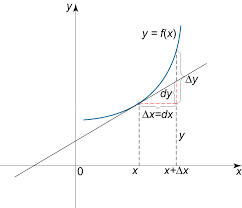
Differentials:

In calculus, the differential represents the principal part of the change in a function y = f(x) with respect to changes in the independent variable. The differential dy is defined by

dy=f'(x)\,dx,

where $f'(x)$ is the derivative of f with respect to x, and dx is an additional real variable (so that dy is a function of x and dx). The notation is such that the equation

dy={\frac {dy}{dx}}\,dx

holds, where the derivative is represented in the Leibniz notation dy/dx, and this is consistent with regarding the derivative as the quotient of the differentials. One also writes

df(x)=f'(x)\,dx.

Tangents and Normal:

Equation of Tangent and Normal:

The angle of intersection of two curves:

More notes on Applications of Derivatives

L Hospital's Rule

limx→4x2−16x−4limx→∞4x2−5x1−3x2In the first limit if we plugged in x=4 we would get 0/0 and in the second limit if we “plugged” in infinity we would get ∞/−∞ (recall that a...

Rolle's Theorem and Mean Value Theorem

Rolle's Theorem:If the function f(x) is1) continuous in the closed interval [a,b]2) differentiable in the open interval (a,b)3) f(a)=f(b)then there exists at least one point c belonging to (a,b) ...