Conic Section: Introduction
Cone:To say it simply, cone is a three-dimensional geometric shape that tapers smoothly from a flat circular base to a point. Mathematically, a surface obtained by generating a generator along a fi...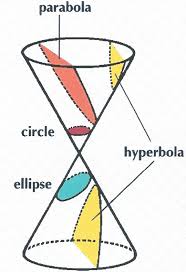

Conic section
A conic section is the intersection of a plane and a cone. By changing the angle and location of intersection, we can produce a circle, ellipse, parabola or hyperbola; or in the special case when the plane touches the vertex: a point, line or 2 intersecting lines.

i) If a plane intersects a cone perpendicular to the axis, then the section is a circle.
ii) If a plane intersects a cone at a given Angle with the axis greater than the semi vertical angle then the section is ellipse.
iii) If an intersecting plane, not passing through the vertex is parallel to the generator of the cone, then the section is a parabola.
iv)if a plane intersects the double right cone such that the angle between the axis and the plane be less then the section is hyperbola.
OR
The locus of a point which moves in a such a way that the ratio of its distance from the fixed point (focus) to its distance from a fixed straight (directrix ) line is constant is called conic section. The constant ratio of focus to directrix is eccentricity.
A conic section in which value of eccentricity is zero is known as circle.
i.e. e=0
A conic section in which value of eccentricity is unity is known as parabola.
i.e. e =1
A conic section in which value of eccentricity is less than unity is known as ellipse.
i.e. e <1
A conic section in which value of eccentricity is greater than unity is known as hyperbola
i.e. e >1
Parabola
The parabola is the curve formed from all the points that are equidistant from the directrix and the focus.
PF/PM=1(constant)

Focal distance: The distance of any point on parabola from the focus F is called focal distance.
Focal chord: Any chord of the parabola passing through the focus is called focal chord.PFP’ is a focal chord.
Latus Rectum: The focal chord which is perpendicular to the axis is called latus rectum.LFL’ is latus rectum.
Equation of parabola in standard form is y2=4ax (important for neb)

To find the equation of parabola in standard form we consider a parabola with vertex at origin and focus at S(a, 0), where a>0. Here axis of parabola is along the x-axis and directrix is parallel to y-axis. Since A is vertex of the parabola so we have AS=AK. Here A is origin so S and K lies on the opposite side so the coordinates of K is K(-a, 0).
Let P(x, y) be any point on the parabola. Draw the perpendicular PM on directrix to meet at M. Now, the coordinate of M is M(-a, y).
By definition of parabola,
PS=PM
Or, (x -a)2+ y2=(x+a)2 +(y-y)2
or, x2 - 2ax + a2+ y2= x2 + 2ax + a2
or, y2=4ax
Different form of parabolas:


| Parabola | focus | axis | Directrix | vertex | Latus rectum |
| y2=4ax | (a,0) | y=0 | x=-a | (0,0) | 4a |
| y2=-4ax | (-a,0) | y=0 | x=a | (0,0) | 4a |
| x2=4ay | (0,a) | x=0 | y=-a | (0,0) | 4a |
| x2=-4ay | (0,-a) | x=0 | y=a | (0,0) | 4a |
| (y-k)2 =4a(x-h) | (h+a,k) | y=k | x=h-a | (h,k) | 4a |
| (x-h)2 =4a(y-k) | (h,k+a) | x=h | y=k-a | (h,k) | 4a |
Some points:
I) A point p(x1,y1) lies outside ,on or inside the parabola y2=4ax according as y12-4ax1 (<=>) 0.
II) parametric equations of parabola y2=4ax are x=at2,y=2at.
𝐸𝑞𝑢𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑡𝑎𝑛𝑔𝑒𝑛𝑡 𝑡𝑜 𝑡ℎ𝑒 𝑝𝑎𝑟𝑎𝑏𝑜𝑙𝑎 𝑦2 = 4𝑎𝑥 𝑎𝑡 𝑎 𝑝𝑜𝑖𝑛𝑡 (𝑥1, 𝑦1)
𝑇ℎ𝑒 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑝𝑎𝑟𝑎𝑏𝑜𝑎𝑙𝑎 𝑖𝑠,
𝑦2 = 4𝑎𝑥
𝑑𝑖𝑓𝑓𝑒𝑟𝑒𝑛𝑡𝑖𝑎𝑡𝑖𝑛𝑔 𝑜𝑛 𝑏𝑜𝑡ℎ 𝑠𝑖𝑑𝑒𝑠 𝑤𝑖𝑡ℎ 𝑟𝑒𝑠𝑝𝑒𝑐𝑡 𝑡𝑜 𝑥
𝑑𝑦/𝑑𝑥=𝑑( 4𝑎𝑥 )/𝑑𝑥
Or,2y𝑑𝑦/dx=4a
Or, dy/dx=(2a/x)
Slope at (x1,y1) is
Or , (dy/dx)(x1,y1)=(2a)/y1
𝑤ℎ𝑖𝑐ℎ 𝑖𝑠 𝑡ℎ𝑒 𝑠𝑙𝑜𝑝𝑒 𝑜𝑓 𝑡𝑎𝑛𝑔𝑒𝑛𝑡 𝑡𝑜 𝑡ℎ𝑒 𝑝𝑎𝑟𝑎𝑏𝑜𝑙𝑎 𝑦
2 = 4𝑎𝑥 𝑎𝑡 (𝑥1, 𝑦1)
m =2𝑎/𝑦1
𝑁𝑜𝑤 𝑡ℎ𝑒 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑡𝑎𝑛𝑔𝑒𝑛𝑡 𝑖𝑠
𝑦 − 𝑦1=2𝑎/𝑦1*(x-x1)
Or, 𝑦𝑦1− y12= 2𝑎𝑥 − 2𝑎𝑥1
Or, 𝑦𝑦1− 4𝑎𝑥1= 2𝑎𝑥 − 2𝑎𝑥1
Or 𝑦𝑦1 = 2𝑎(𝑥 + 𝑥1)
𝐶𝑜𝑛𝑑𝑖𝑡𝑖𝑜𝑛 𝑡ℎ𝑎𝑡 𝑎 𝑙𝑖𝑛𝑒 𝑦 = 𝑚𝑥 + 𝑐 𝑖𝑠 𝑎 𝑡𝑎𝑛𝑔𝑒𝑛𝑡 𝑡𝑜 𝑡ℎ𝑒 𝑝𝑎𝑟𝑎𝑏𝑜𝑙𝑎 𝑦2 = 4𝑎𝑥. 𝐹𝑖𝑛𝑑 𝑡ℎ𝑒 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑡𝑎𝑛𝑔𝑒𝑛𝑡 𝑡𝑜 𝑡ℎ𝑒 𝑝𝑎𝑟𝑎𝑏𝑜𝑙𝑎 𝑦2 = 4𝑎𝑥 𝑖𝑛 𝑡ℎ𝑒 𝑠𝑙𝑜𝑝𝑒 𝑓𝑜𝑟𝑚. 𝐴𝑙𝑠𝑜𝑓𝑖𝑛𝑑 𝑡ℎ𝑒 𝑝𝑜𝑖𝑛𝑡 𝑜𝑓 𝑐𝑜𝑛𝑡𝑎𝑐𝑡.
𝑃𝑟𝑜𝑜𝑓: 𝑠𝑢𝑝𝑝𝑜𝑠𝑒 𝑦 = 𝑚𝑥 + 𝑐 𝑖𝑠 𝑎 𝑡𝑎𝑛𝑔𝑒𝑛𝑡 𝑡𝑜 𝑡ℎ𝑒 𝑝𝑎𝑟𝑎𝑏𝑜𝑙𝑎 𝑦2 = 4𝑎𝑥.
𝑠𝑜𝑙𝑣𝑖𝑛𝑔 𝑦 = 𝑚𝑥 + 𝑐 𝑎𝑛𝑑 𝑦2 = 4𝑎𝑥.
(𝑚𝑥 + 𝑐 )2 = 4𝑎𝑥
𝑜𝑟, (𝑚x)2 + 2𝑚𝑐𝑥 + 𝑐2 − 4𝑎𝑥 = 0
𝑜𝑟, 𝑚2𝑥2 + 2 𝑚𝑐 − 2𝑎 𝑥 + 𝑐2 = 0
𝑤ℎ𝑖𝑐ℎ 𝑖𝑠 𝑞𝑢𝑎𝑑𝑟𝑎𝑡𝑖𝑐 𝑖𝑛 𝑥 𝑎𝑛𝑑 𝑦 = 𝑚𝑥 + 𝑐 𝑖𝑠 𝑡𝑎𝑛𝑔𝑒𝑛𝑡 𝑜𝑓 𝑦2= 4𝑎𝑥, 𝑠𝑜 𝑡ℎ𝑒 𝑑𝑖𝑠𝑐𝑟𝑖𝑚𝑖𝑛𝑎𝑛𝑡 𝑖𝑠 𝑧𝑒𝑟𝑜. 𝑖. 𝑒.𝑡ℎ𝑒 𝑣𝑎𝑙𝑢𝑒 𝑜𝑓 𝑥 𝑎𝑟𝑒 𝑒𝑞𝑢𝑎𝑙.
4 (𝑚𝑐-a)2 − 4𝑚2c2=0
𝑜𝑟, (𝑚c)2 − 𝑎𝑐𝑚 + 𝑎2 − 𝑚2𝑐2 = 0
𝑜𝑟, −4𝑎𝑐𝑚 + 4𝑎2= 0
𝑜𝑟, 𝑐𝑚 = 𝑎
𝑜𝑟, 𝑐 =𝑎/𝑚
𝑤ℎ𝑖𝑐ℎ 𝑖𝑠 𝑡ℎ𝑒 𝑟𝑒𝑞𝑢𝑟𝑒𝑑 𝑐𝑜𝑛𝑑𝑖𝑡𝑖𝑜𝑛 𝑓𝑜𝑟 𝑦 = 𝑚𝑥 + 𝑐 𝑡𝑜 𝑏𝑒 𝑎 𝑡𝑎𝑛𝑔𝑒𝑛𝑡.
𝑎𝑛𝑑 𝑡ℎ𝑒 𝑡𝑎𝑛𝑔𝑒𝑛𝑡 𝑖𝑛 𝑠𝑙𝑜𝑝𝑒 𝑓𝑜𝑟𝑚 𝑖𝑠 𝑦 = 𝑚𝑥 +𝑎/m
𝑝𝑜𝑖𝑛𝑡 𝑜𝑓 𝑐𝑜𝑛𝑡𝑎𝑐𝑡: 𝐼𝑛 𝑡ℎ𝑒 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛 𝑦𝑦1 = 2𝑎 (𝑥 +𝑥1) ,( 𝑥1,𝑦1) 𝑖𝑠 𝑝𝑜𝑖𝑛𝑡 𝑜𝑓 𝑐𝑜𝑛𝑡𝑎𝑐𝑡
𝑦𝑦1 = 2𝑎 𝑥 + 𝑥1 𝑐𝑎𝑛 𝑏𝑒 𝑤𝑟𝑖𝑡𝑡𝑒𝑛 𝑎𝑠
2𝑎𝑥 − 𝑦𝑦1 + 2𝑎𝑥1 = 0 … … . . (𝑖)
𝑎𝑛𝑑 𝑡ℎ𝑒 𝑡𝑎𝑛𝑔𝑒𝑛𝑡 𝑖𝑛 𝑠𝑙𝑜𝑝𝑒 𝑓𝑜𝑟𝑚 𝑖𝑠 𝑦 = 𝑚𝑥 +a/𝑚
𝑜𝑟, 𝑚𝑥 − 𝑦 +𝑎/m= 0 … … … 𝑖𝑖
𝑠𝑢𝑝𝑝𝑜𝑠𝑒 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛 𝑖 𝑎𝑛𝑑 𝑖𝑖 𝑟𝑒𝑝𝑟𝑒𝑠𝑒𝑛𝑡 𝑠𝑎𝑚𝑒 𝑡𝑎𝑛𝑔𝑒𝑛𝑡
2𝑎/𝑚=−𝑦1/−1=2𝑎𝑥1/(𝑎/m)
𝑓𝑟𝑜𝑚 𝑓𝑖𝑟𝑠𝑡 𝑡𝑤𝑜 𝑟𝑎𝑡𝑖𝑜
2𝑎/𝑚=𝑦1/1
𝑜𝑟, 𝑦1=2𝑎/𝑚
𝑡𝑎𝑘𝑖𝑛𝑔 𝑓𝑖𝑟𝑠𝑡 𝑎𝑛𝑑 𝑙𝑎𝑠𝑡 𝑟𝑎𝑡𝑖𝑜
Or,2𝑎/𝑚=2𝑎𝑚𝑥1/𝑎
𝑜𝑟 𝑥1 =𝑎/𝑚2
𝐻𝑒𝑛𝑐𝑒 𝑡ℎ𝑒 𝑝𝑜𝑖𝑛𝑡 𝑜𝑓 𝑐𝑜𝑛𝑡𝑎𝑐𝑡 𝑖𝑠( 𝑎/𝑚2,2𝑎/𝑚)
slope of tangent = 2𝑎/𝑦1
slope of normal =−𝑦1/2𝑎
the passing point of the normal is( 𝑥1, 𝑦1)
the equation of normal is
𝑦−𝑦1 =(−𝑦1/2𝑎)(𝑥 − 𝑥1)
Equation of normal in slope form
the equation of normal is
𝑦−𝑦1 =(−𝑦1/2𝑎)(𝑥 − 𝑥1) ………(i)
let, 𝑚 =−𝑦1/2𝑎
or, 𝑦1 = −2𝑎𝑚
since (𝑥1, 𝑦1) lies on 𝑦2= 4𝑎𝑥
𝑦12 = 4𝑎𝑥1
(−2𝑎𝑚)2 = 4𝑎𝑥1
𝑥1 = 𝑎𝑚2
from (i)
𝑦 + 2𝑎𝑚 = 𝑚(𝑥 − 𝑎𝑚2)
𝑦 = 𝑚𝑥 − 2𝑎𝑚 − 𝑎𝑚3
which is required equation of normal in normal form.
Equation of tangent and normal to the parabola in parametric form
Proof: The equation of parabola is 𝑦2 = 4𝑎𝑥
and the point of contact (𝑎𝑡2, 2𝑎𝑡)
Putting this point in equation yy1=2a(x-x1) we get
y*2at=4a*(x-at2)
Or yt=x+at(eqn of tangent)
𝑦 + 𝑡𝑥 = 2𝑎𝑡 + 𝑎𝑡(eqn of normal)