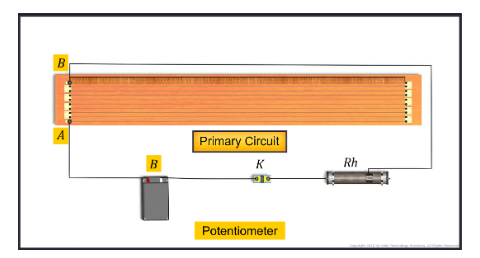
It is an electronic device that measure accurate resistance of the conductor. it measures unknown resistance with the help of known resistance. Let P, Q and R are three known resistance and X be the unknown resistance are connected in quadrilateral closed electric circuit and the two junctions of the quadrilateral are connected with battery and the remain two junctions are connected galvanometer and the deflection was not shown by the galvanometer. These conditions are called balance conditions.

At this condition,

Ig= 0.at this condition

PQ==XR

Determination for the balanced condition for the bridge: to determine the balance condition the arrangement is shown in the figure.

Let us consider the 4 resistance in are arrange in quadrilateral from when it is connected with battery then current is divided into two-part i.e I1 and I3 passes through the resistance P and Q. similarly I2 and I4 pass through resistance X and R respectively.

From the second law of Kirchhoff’s law for the closed-loop ADBA we have

I₁P + IgRg= I₂X……………..1

Similar to closed-loop BDCB we have,

I₃ Q = IgRg + I₄R………2

Again from the first law of Kirchhoff’s at point D

I₂+ Ig=I4………3,

Similarly at B we have

I₁ = Ig +I₃………………4

Now at balance condition Ig=0 and no current passes through the galvanometer then above equation 1, 2, 3, and 4. Become.

I₁P +0xR_g= I₂X……………..5

I₁P =I₂X

I₃ Q = 0xR_g +I₄R………6

I1=I3………7

I2 = I4………………8

Dividing eq. 5 by 6 we have

(I1P/I3Q) = (I2X/I4R)……..9

Now from equation from 7, 8, and 9 we have

P/Q = X/R

This is the expression for the balance condition of the Wheatstone bridge.