Conic Section: Parabola
In this note, we will discuss:Parabola, Some terminology, Standard Equation of parabola and its different forms, Equation of parabola with its axis parallel to x-axis, General E...
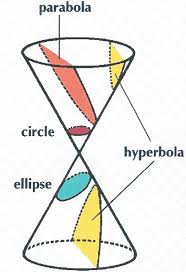
Cone:
To say it simply, cone is a three-dimensional geometric shape that tapers smoothly from a flat circular base to a point.
Mathematically, a surface obtained by generating a generator along a fixed line such that the semi vertical angle (vertex angle) is always fixed, is called a cone (or right cone).

We take double right cone for our better understanding.
Now, a surface obtained by the intersection of a cone (or right cone) with a plane is called conic section. The nature of conic sections (i.e. curves) depends upon the position of intersection of a cone and a plane:

· If the angle between plane and axis of cone is right angle then the conic section is a circle.
· If the angle between plane and axis of cone is greater than the semi vertical angle then the conic section is an ellipse.
· If the plane cuts the cone parallel to a generator then the conic section is a parabola.
· If the angle between plane and axis of cone is less than the semi vertical angle then the conic section is a hyperbola.

Conic Section:
We can define conic section as, a locus of a point which moves in a plane such that the ratio of distances from a fixed point to a fixed straight line is always a fixed constant. The fixed point is called focus. The fixed line is called directrix. The ratio of distances is called eccentricity(e).

Now, on the basis of eccentricity; if:
<If you find any difficulty or mistake, do reach out to me through the comment section or social media.>
<notes source: from Rakesh Kumar Jha (RK) sir and book>
<images from internet>