Photoelectric Effect: Introduction

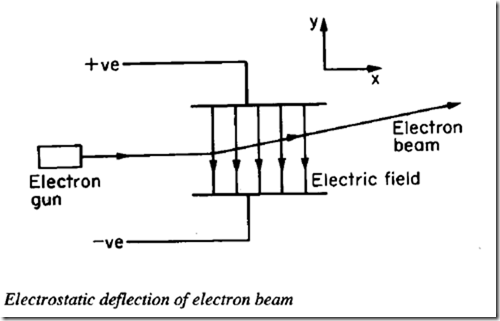
Motion of Electron Beam in Electric Field

Let us consider two plates having potential difference 'V', then electric field is generated from +ve to -ve terminal. Let the length of plate be 'D' and distance between two plates be 'd.' Now, a beam of electron moving with a velocity of 'v' enters region between plates as shown in figure. Due to inertial property one component of force on beam acts along it's original direction i.e. along horizontal direction for this diagram & other force i.e. force of attraction due to electric field acts along +ve part of plate as electrons are -ve charged. These two forces combine to produce a parabolic path.
Considering at point F, electron beam covers 'x' horizontal distance and 'y' vertical distance.
We know that,
E=V/d
or, F(Electrostatic force of attraction for one electron)=Ee
or, F=eE.......(i)
And,
F=ma(m=mass of an electron, a=acceleration of electron beam due to vertical component)......(ii)
From (i) and (ii)
ma=eE
or, a=eE/m.....(a)
The horizontal component of force doesn't produce any acceleration,
v(horizontal)=initial velocity of beam=v
or, v=x/t
or, t=v/x..........(b)
Similarly,
y=v(vertical)t+(1/2)at^2
Since, the initial velocity's horizontal component is zero, so v(vertical)=0,
or, y=(1/2)at^2
From (a) and (b)
y=(1/2)*(eE/m)*(v/x)^2
or, y=(eV/2mdv^2)x^2
or, y=kx^2(as eV/2mdv^2 are constant)
which is equation of parabola.
Hence, the path of electron beam in electric field is parabolic.
Let us consider that beam of electron just eject out as shown in figure with velocity of v' making an angle of θ with horizontal.
Now, t=v/D
v'(horizontal component)=v=D/t......(iii)
v'(vertical component)=v(vetical)+at [v(vertical)=0]
or, v'(vertical component)=(eE/m)*t
or, v'(resultant)=(v'(horizontal)^2+v'(vertical)^2)^1/2
=((D/t)^2+(eEt/m)^2)^1/2...........(c)
Now,
tan θ =v(vertical)/v(horizontal)
or, tan θ=(eEt^2)/mD
or, tan θ=(eVD/mdv^2) (where, E=V/d)......(d)
Therefore, the velocity of ejection of electron from plate and angle made by the direction of velocity to it's horizontal component is identified.