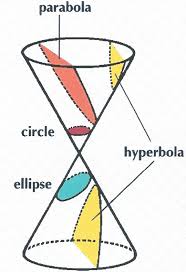
Ellipse

An ellipse is the locus of the point such that its distance from the focus bears the constant ratio to the distance from the line called directrix .the value of eccentricity lies between the 0 and 1

Equation of an ellipse in standard form

x2a2+y2b2x2a2+y2b2= 1

 When the center of an ellipse is ( h, k)

(x−h)2a2+(y−k)2b2(x−h)2a2+(y−k)2b2= 1

Hyperbola

A hyperbola is a set of all points in a plane such that the difference of the distances from the two fixed points called foci is a constant.

Equation of the hyperbola in a standard form is given byx2a2−y2b2x2a2−y2b2= 1 centre at origin C (0, 0) foci = (± ae, 0) directrix ,x =± aeae

 Length of latus rectum =2b2a