Important relations in Circular Motion


Circular Motion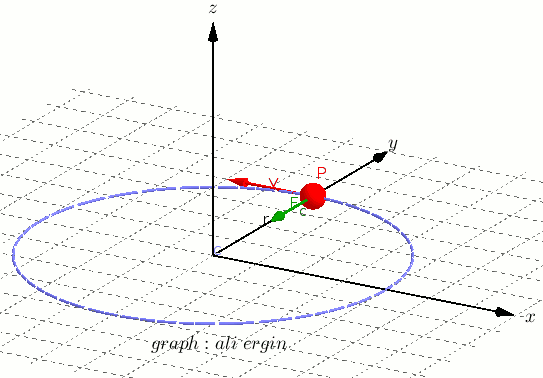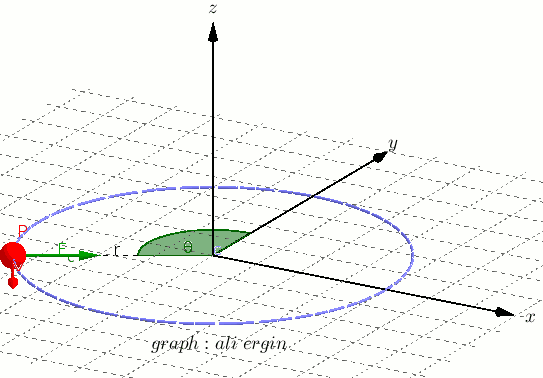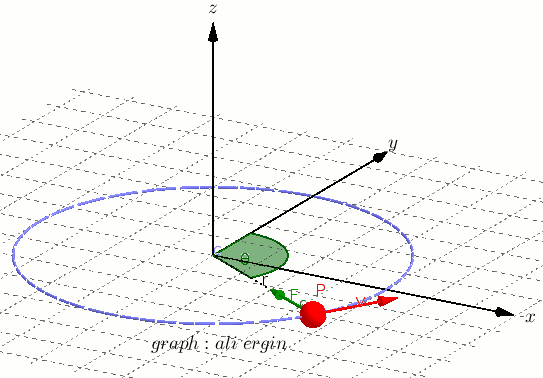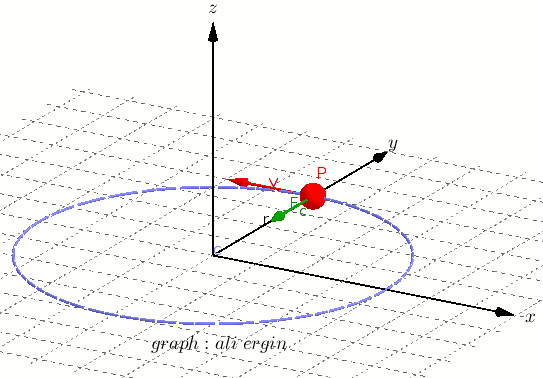

↪ An object is said to be in circular motion if the motion of the object in a plane is such that its distance from a fixed point remains constant.
↪ The path of the object is called a circle and the fixed point is called the center.
↪ The least distance of the object from the center is called the radius of the circular path.
 Suppose an object is moving in a circle of radius r and center O with a certain speed.
Suppose an object is moving in a circle of radius r and center O with a certain speed.
⁕ Angular Displacement
↪ If the object moves from point A to point B, then it describes an angular displacement θ about O.
⁕ Angular Velocity
↪ The angular velocity of the object is defined as the angular displacement per second.
↪ If t is the time taken to describe an angular displacement θ, then

↪ In SI, the angle or angular displacement is measured in radians (rad).
↪ So the angular velocity is measured in radians per second (rad/s).

↪ This is analogous to S = ut for motion in a straight line.
↪ If S is the length of an arc AB, then from the definition of a radian angle,

Dividing both sides of it by t (time taken to move from point A to B), we get

where v is the linear velocity of the object in circular motion.
↪ Equation (3) gives the relation between the linear and angular velocity.
⁕ Time period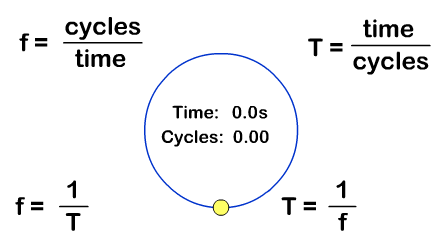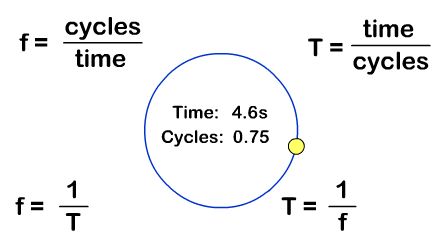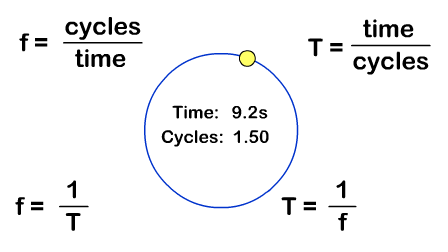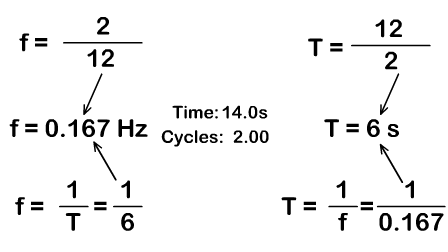
↪ The period of the object in circular motion is defined as the time taken by it to make one complete revolution.
↪ It is denoted by T. In one complete revolution, it describes an angular displacement of 2π radians.
So from (1), we get

↪ This is the period of revolution.
⁕ Frequency
↪ The frequency of revolution of the object is defined as the number of revolutions made per second.
↪ It is denoted by f and is measured in revolutions per second (rev/s).
↪ Since f number of revolutions are made in 1 s, then 1 number of revolution is made in 1/f s.
↪ From the definition, the time taken to make one complete revolution is the period, T.

↪ This is the relation between the angular velocity and frequency.
Relation between Linear and Angular Acceleration
↪ Suppose an object is moving in a circle of radius r and center O. If the angular velocity of the object increases from ωo to ω in time t, the angular acceleration is 

↪ If v and u are the corresponding final and initial linear velocities, then

where a is the linear acceleration.
↪ Equation (1) gives the relation between the linear and angular acceleration.