Introduction of Elasticity
↪ Elasticity is a fundamental property of all matter by virtue of which an object regains its original shape and size when a deforming force is removed.↪ When the deforming force is appl...

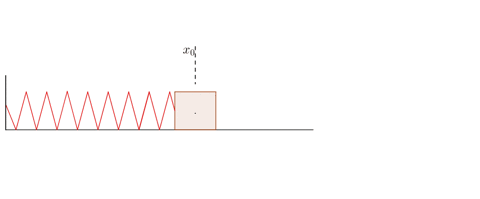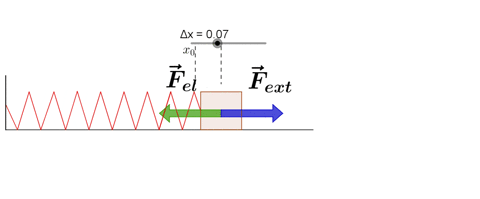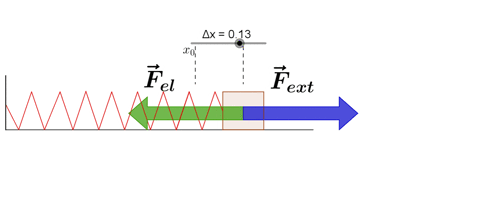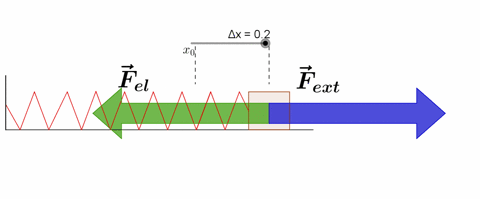
Hooke's Law

↪ Elbert Hooke studied the elastic behavior of different objects.
↪ He observed for relatively small deformations of an object, the size of the deformation is directly proportional to deforming force.
↪ He summed up his findings in 1676, which is known as Hooke's law.
Hooke's law states that, "Restoring force acting on a body is directly proportional to extension produced within the elastic limit."
That is,
F ∝ x
F = -kx
where k is force constant or spring constant and x is extension produced.
↪ Within elastic limit, the object returns to its original shape and size upon removal of the load.
↪ The value of k depends upon on the nature of elastic material and also on its shape and dimensions.
↪ It is number that represents how much force it takes to stretch a material.
Experimental Verification of Hooke's Law
 Fig: Experimental verification of Hooke's Law
Fig: Experimental verification of Hooke's Law
↪ Suspend a metallic spring AB vertically from a rigid support and attach a scale pan to the lower end B.
↪ Fix a pointer P near the end B of the spring which can slide over a fixed vertical scale B as shown in figure.
↪ When the scale pan is empty note the reading.
↪ Add some known weight on pan and then note the reading again.
↪ The difference in these two readings will give us the extension in the spring.
↪ Go on adding the weights step by step on pan.
↪ Plot a graph between the weight on the pan and extension on the spring.
↪ The graph will be a straight line.
This shows that
extension ∝ load applied
Thus Hooke's Law is verified.
Interatomic Forces
↪ The inter-atomic forces are electrical in nature.
↪ Such forces are active if the distance between the atoms is of the order of atomic size (10-10 m)
↪ An atom consists of a positively charged nucleus around which the negatively charged electrons resolve in certain definite orbitals.
↪ The positive charge on the nucleus if an atom is equal to the negative charge due to electrons.
↪ Hence the atom is electrically neutral.
↪ The inter-atomic force increases as the distance between atoms decreases.
↪ When the distance between two atoms is very small, then the electrons clouds of two atoms start overlapping and the inner atomic force become repulsive.
↪ The variation of interatomic force with distance is shown below:

↪ The interatomic force is equal to the negative gradient of the corresponding potential energy function.
F = - dU(r)/dr
Intermolecular Forces
↪ The force which is responsible to hold together the atom or molecules of a matter is called intermolecular force.
↪ When two molecules are far from each other, the force between them is attractive in nature and negligible.
↪ It has been found that the intermolecular force of attraction is inversely proportional to the seventh power of the distance between the molecules.
Fa ∝ 1/r7
or, Fa = - A/r7
where A is constant related to the nature of molecules and negative sign indicates that the force is attractive in nature.
As the distance between the molecules is decreased and made equal to the order of the dimension of the molecule, they began to repel each other.
↪ The force of repulsion varies inversely as the ninth power of the intermolecular separation.
Fr ∝ 1/r9
or, Fr ∝ B/r9 where B is constant related to the nature of the molecule.
Thus the net force acting on a molecule is given by
F = A/r7 + B/r9
↪ There is a definite distance ro between the molecules at which the force of attraction ad repulsion balance and the molecules are in the state of stable equilibrium.
i.e.,
F = 0 at r = ro
ro = √(B/A)
Elastic Behavior of Solids
↪ In solids, atoms and molecules are arranged in such a way that such molecules is acted upon by the forces due to the neighboring molecules.
↪ These forces are known as intermolecular forces.
↪ When no force is applied each molecules are in equilibrium.
↪ When it is slightly pulled its length increases. In other word, the solid is deformed.
↪ This force is deforming force and when it is removed the body gains original shape and size.
↪ The force responsible to bring the spring to its original state is reforming force.
Elastic Limit
↪ Elastic limit is the upper limit of deforming force up to which if deforming force is removed, the body regains its original form completely and beyond which if deforming force is increased, the body loses property of elasticity and gets permanently deformed.