Progressive Wave

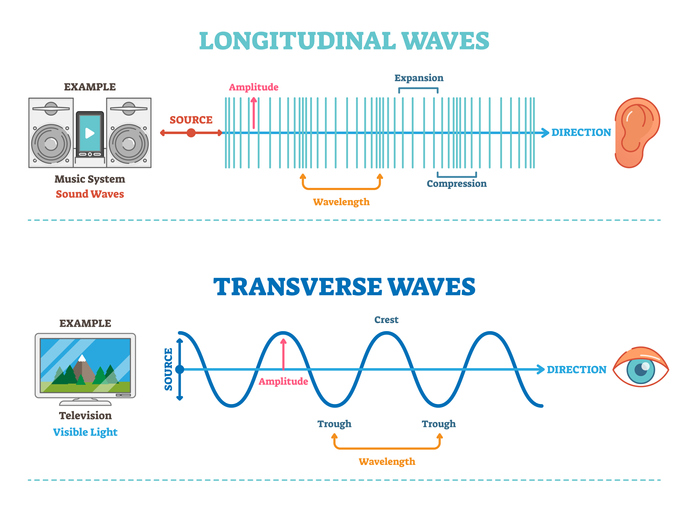
If the wave profile moves along the forward direction with the speed of the wave, it is called a progressive wave. Both transverse and longitudinal waves are progressive waves. The amplitude and frequency of vibration of particles in a progressive wave are the same but the phase of the vibration changes point to point along the wave.

Progressive wave equation:

Suppose, the wave moves from left to right with displacement velocity v in which each article vibrates with simple harmonic motion. But successive particles to the right have phase lag as compared to the motion of the particle o at the origin O (at x = 0). The displacement y of the vibrating particle at origin O is given by,

y = a sin ωt ......... (1)

where 'a' is amplitude, 't' is time:
ω = 2πf, is the angular velocity, where f is the frequency of vibration.

Consider a particle P at distance x from the origin as in fig.

Φ be the phase lag of the particle P and λ be the wavelength.

At a distance λ from O, phase difference, Φ = 2π
At a distance x from O, phase difference, Φ = (2π/λ)*x

The displacement of the particle P at distance x from O is,

Equations (2), (3), and (4) are different forms of the plane-progressive wave equation, for a wave that moves from left to right so the vibration of particle P lags on that at O. If a wave is traveling from right to left then the waves arrive at P before O, therefore vibration of P leads that at O. In such a case, will be positive and wave equation is given by,

y = a sin (ωt + kx) ......... (5)

The particle velocity v for the particle at fixed distance x from O is obtained by taking the derivative of y with respect to t (taking x constant),