Lens Formula
It is a relationship between the focal length of a lens and distances of object and image from the optical center of the lens. To derive this formula we use the following sign conventions.
1. All distances are measured from the optical center of the lens.
2. Real distances are taken as positive and virtual distances are taken as negative.
3. For a convex lens, f is positive and for a concave lens, f is negative.
4. For a real image, magnification M is positive and for a virtual image, magnification M is negative.
Convex lens
The image formed may be real or virtual.
1. (i) Real image (extended object method)
Let us consider a convex lens as shown in figure. Let O be the optical centre and F be the principal focus of a convex lens of focal length OF=f.
Let AB be and extended object placed in between F and 2F of the lens as shown in figure.
AB is held perpendicular to the principal axis of the lens. A real, inverted and magnified image A'B' is formed beyond 2F as shown in figure.
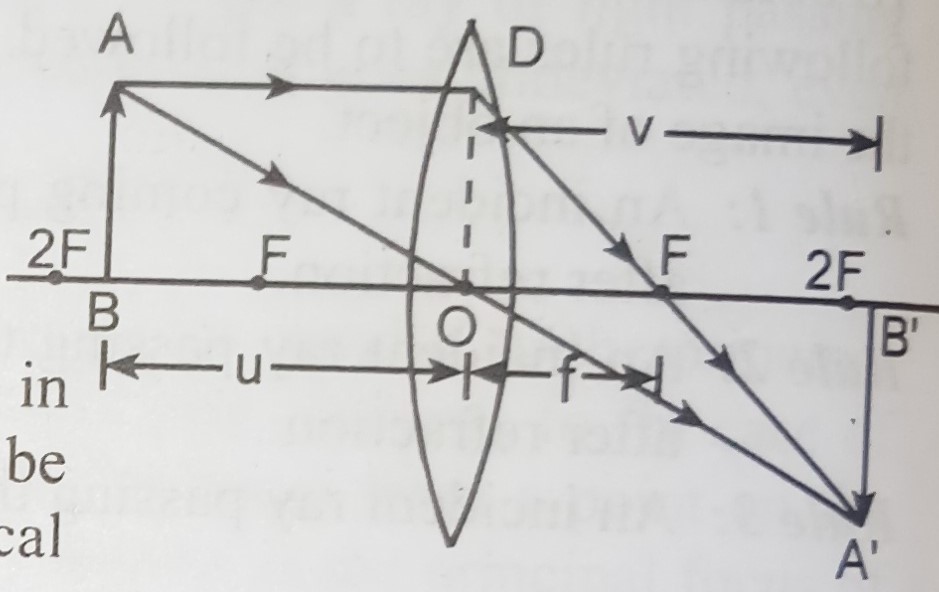
As A'B'O and ABO are similar,
A'B'/AB = OB'/OB …………………… eq(n) (1)
Again A'B'F and ODF are similar,
A'B'/OD = FB'/OF …………………… eq(n) (2)
But OD = AB,
A'B'/OD = FB'/OF …………………… eq(n) (3)
From equations (1) and (3),
OB'/OB = FB'/OF = (OB^'-OF)/OF
Using sign conventions,
OB = u, real object distance
0B' = v, real image distance
OF = f, focal length of lens
So, v/u = (v-f)/f
or, vf - uv = uf
or, uv = uf+ vf
Divide both sides by uvf,
uv/uvf = uvf/uvf + vf/uvf
or, 1/f = 1/v + 1/u is the required equation.
(ii) Real image (point object method)
Consider a thing convex lens as shown in Figure. Let C be the optical centre of lens. Thin lens can be supposed to be made up of large number of small angle prisms, and XYZ is one of such prisms. In small angle prism, deviation produced is independent of angle of incidence.
Consider real point object O on the principal axis of the lens. A ray of light OX incident on the lens gets refracted and passes through point I as shown in Fig (i). Another ray of light OC passing through optical centre goes without bending. Two refracted rays intersect at I. Hence, I is the real image of O. If there were no lens, ray OX would travel along ON as shown in Fig.(i).Let M be a point at a height h above C as shown in Fig. (i) and (ii).
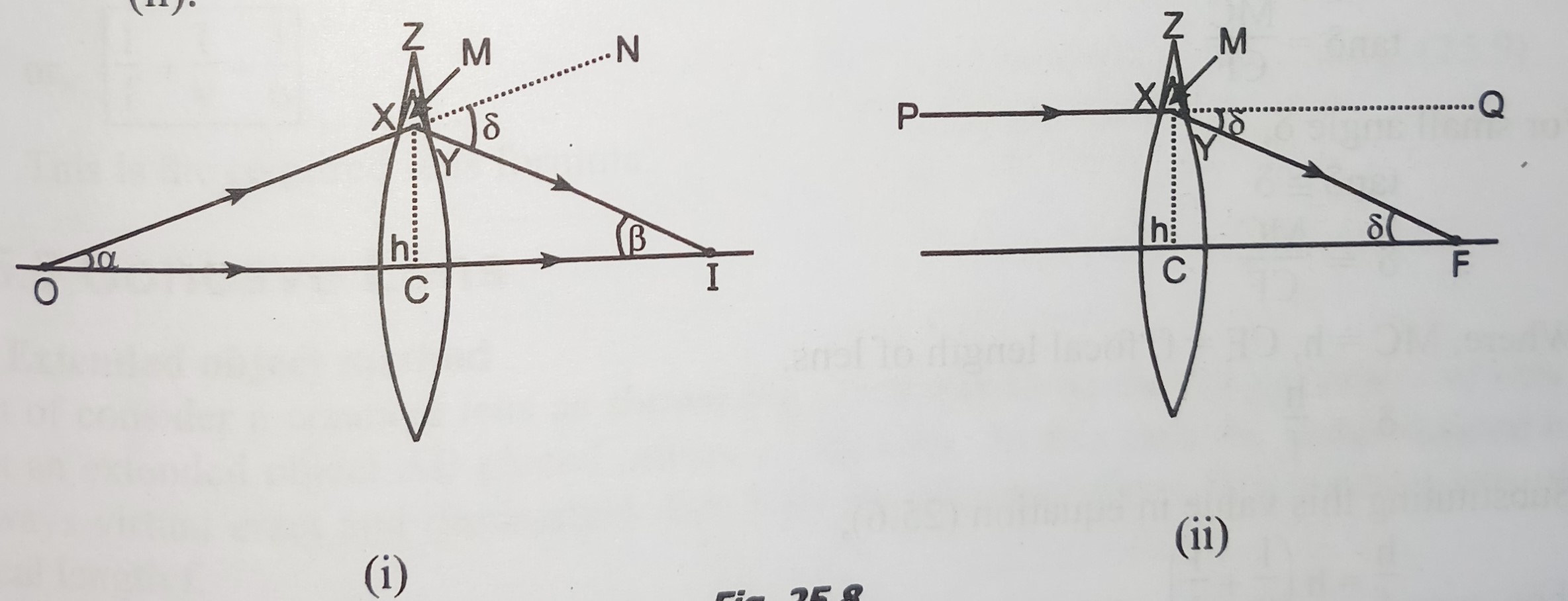
In Fig.(i).
NMI = δ: angle of deviation.
Let angle MOC = α, MIC = β.
From Fig.(i)
δ = α + β ……………………………………… Eq(n) 1 (Exterior angle)
From Fig. tanα = MC/OC
Tanβ = MC/IC
For small angles α and β,
Tan α ≈ α, Tan β ≈ β,
So, α = MC/OC and β = MC/IC
Substituting these values in equation (1),
β = MC/OC + MC/IC
Where MC = h
OC = u, real object distance
IC = v, real image distance
So, β = h/u + h/v ….........………Eq(n)2
Another ray of light PX parallel to the principal axis passed through focus after refraction as shown in Fig. (ii). If there were no lens, ray PX would travel along PQ.
In Fig. (ii)
QMF = δ
From Fig, MFC = QMF = δ (Alternate angles)
From Fig. (ii)
Tanδ = MC/CF
For small angle δ,
Tanδ ≈ δ
δ = MC/CF
Where, MC = h, CF = f, focal length of lens.
δ = h/f
Substituting this value in equation (2),
h/f = h/u + h/v
So, 1/f = 1/u + 1/v is the required equation.
Virtual image
Consider an extended object AB placed infront of a convex lens. Let O be the optical centre of the lens. When the object AB is held close to the lens between O and F the image A'B' formed by convex lens is virtual, erect and magnified.
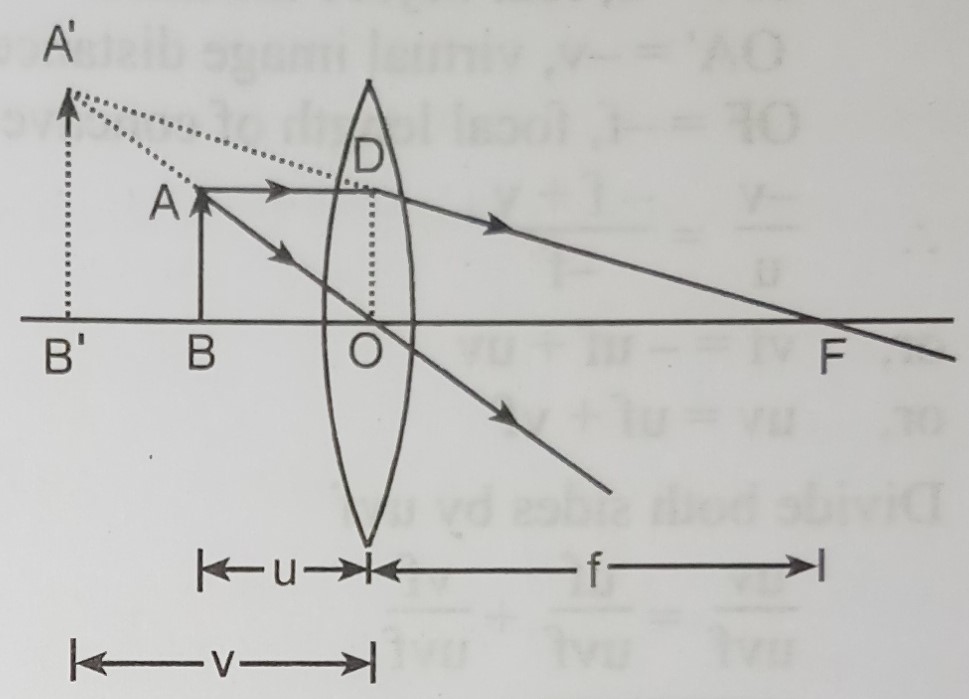
As A'B'O and ABO are similar,
A'B'/AB = OB'/CB …………………… eq(n) (1)
Again A'B'F and ODF are similar,
A'B'/OD = FB'/OF …………………… eq(n) (2)
But OD = AB,
A'B'/OD = FB'/OF …………………… eq(n) (3)
From equations (1) and (3),
OB'/OB = FB'/OF = (OB^'+OF)/OF
Using sign conventions,
OB = u, real object distance
OB' = -v, virtual image distance
OF = f, focal length of lens
So, (-v)/u = (-v+f)/f
or, -uv + uf = -vf
or, uv = uf+ vf
Divide both sides by uvf,
uv/uvf = uvf/uvf + vf/uvf
or, 1/f = 1/v + 1/u is the required equation.







