Force on moving charge in a magnetic field

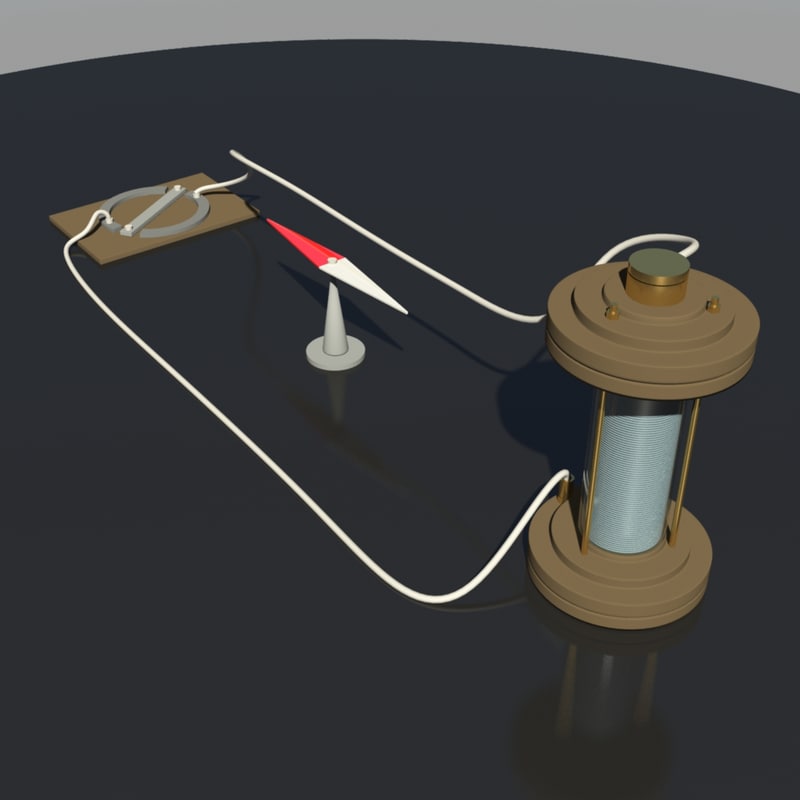
Consider a moving unit positive charge is placed in a magnetic field B with charge +q moving with velocity v making angle θ with the magnetic field. 
Here, the charge experiences a force that is perpendicular to the plane of B and v. Experimentally it is found that magnitude of magnetic force F is:

1. 
   directly proportional to the magnitude of the charge 
   F ∝ q
   
   
   


2. directly proportional to the velocity of the charge
   F ∝ v
   
   
   


3. directly proprtional to strength of magnetic field
   F ∝ B
   
   
   


4. directly proportional  to sine of angle between v and B
   F ∝ sinθ

Combining above equations, we get 

     F ∝ qvBsinθ
or, F = kqvBsinθ
where, k is proportionality constant and its value is 1 in SI - units. So, we have force,

F = qvBsinθ

In vector form,

The force is perpendicular toand. This force is called Lorentz magnetic force. We see that F is perpendicular to the plane containing v and B.

Since F acts perpendicular to v and B, so F is a deflecting force. It doesn't change the magnitude of v, but change the direction of motion of the charge when it enters the field B. Since F is perpendicular to displacement of charge, no work is done by F. So, no energy is gained by the charge when it enters the field B and F acts on it.

Reference taken from ' Principle of Physics' - Ayam Publication