Electric Flux and Gauss's Law
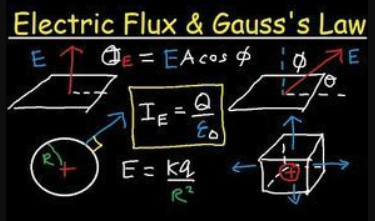
Electric Flux
The product of the magnitude of the electric field and surface area perpendicular to the field is called the electric flux.
From the SI units of E and A, we see that has units of newton meters squared per coulomb (N .m2/C). Electric flux is proportional to the number of electric field lines penetrating some surface.
We see that the flux through a surface of fixed area A has a maximum value EA when the surface is perpendicular to the field (when the normal to the surface is parallel to the field, that is, when Ɵ = 0°); the flux is zero when the surface is parallel to the field (when the normal to the surface is perpendicular to the field, that is, when Ɵ = 90°).
In this discussion, the angle Ɵ is used to describe the orientation of the surface of area A.
Gauss’s Law
The net flux through any closed surface surrounding a point charge q is given by q/
and is independent of the shape of that surface.

where represents the electric field at any point on the surface and qin
represents the net charge inside the surface.
A gaussian surface is an imaginary surface you construct to satisfy the conditions listed here. It does not have to coincide with a physical surface in the situation.
In choosing the surface, always take advantage of the symmetry of the charge distribution so that can be removed from the integral. The goal in this type of calculation is to determine a surface for which each portion of the surface satisfies one or more of the following conditions:
1. The value of the electric field can be argued by symmetry to be constant over the portion of the surface.
2. The dot product in Equation  can be expressed as a simple algebraic product E dA because
can be expressed as a simple algebraic product E dA because and
are parallel.
3. The dot product in Equation  is zero because
is zero because and
are perpendicular.
4. The electric field is zero over the portion of the surface.