Stationary Wave

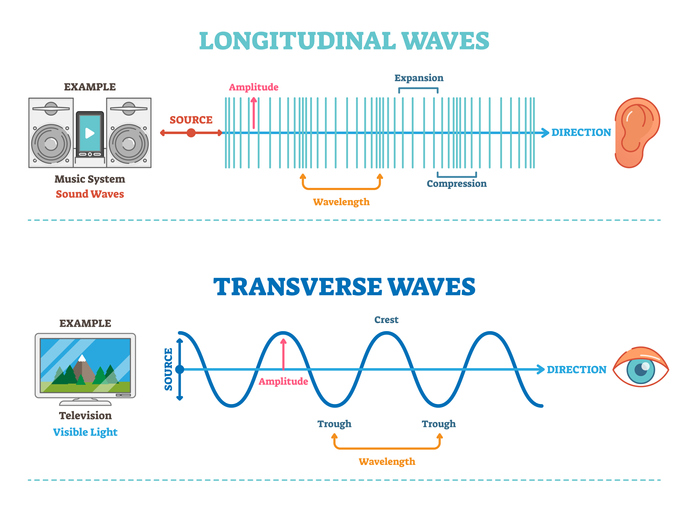
When two waves of the same frequency, velocity, wavelength, and amplitude but traveling in the opposite direction will superimpose, it gives rise to a new wave which is called a stationary wave. It is also called a standing wave.
This wave doesn't carry any energy. It has nodes and antinodes. Node is the position of zero vibration and antinode is the position of maximum vibration.

Principle of superposition of wave:
If two or more than two waves move in a medium simultaneously then the resultant displacement is given by the algebraic or vectorial sum of individual displacement.

Stationary wave equation:

Let us consider two waves moving in a medium simultaneously as shown in the figure. The equation of wave that moves from left to right and from right to left is given by y1 and y2 respectively. Let y be the resultant displacement.

Then,

y₁= a sin(ωt - kx) ........... (1)

y₂= a sin(ωt + kx) .......... (2)

By principle of superpiosition of waves,

y = y₁ + y₂
y = asin(ωt+kx) + asin(ωt-kx)
y = 2a.sin[(ωt+kx + ωt-kx)/2].cos[(ωt+kx - ωt+kx)/2]
y = 2a.sinωt.coskx
y = A sinωt    where, A = 2a.coskx is amplitude

For minima (node):
A = 0
2acoskx = 0
coskx = 0
kx= (2n+1)π/2
2.2kx = (2n+1)π
2.(2π/λ) = (2n+1)π    where, λ = wavelength
x= ¼×(2n+1)×π

This is the condition for node formation.
If n = 0, 1, 2, 3 .....
x= λ/4, 3λ/4, 5λ/4, .....

For maxima (antinode):
coskx= +1 or -1
coskx =cosnλ
kx= nλ
2πx/λ = nπ
x= nλ\2

This is the condition for antinode formation .
If n= 0, 1, 2, 3, .....
x = 0, λ/2, λ, 3λ/2, .....

So,
antinode - antinode = ∆/2
node - node = ∆\2
node - antinode = ∆/4