ask
mattrab
Visit www.askmattrab.com for more academic resources.
Introduction To Equilibrium
Equilibrium
An object is in equilibrium if the linear momentum of its center of mass is constant and if its angular momentum about its center of mass is constant:
P = constant
L = constant
An object is in static equilibrium if its linear momentum and angular momentum is equal to zero:
P = 0 kg m/s,
L = 0 kg m2/s
CONDITIONS FOR EQUILIBRIUM
We say that a rigid body is in equilibrium when both its linear and angular acceleration are zero relative to an inertial frame of reference. This means that a body in equilibrium can be moving, but if so, its linear and angular velocities must be constant. We say that a rigid body is in static equilibrium when it is at rest in our selected frame of reference. Notice that the distinction between the state of rest and a state of uniform motion is artificial—that is, an object may be at rest in our selected frame of reference, yet to an observer moving at constant velocity relative to our frame, the same object appears to be in uniform motion with constant velocity. Because the motion is relative, what is in static equilibrium to us is in dynamic equilibrium to the moving observer, and vice versa. Since the laws of physics are identical for all inertial reference frames, in an inertial frame of reference, there is no distinction between static equilibrium and equilibrium.
According to Newton’s second law of motion, the linear acceleration of a rigid body is caused by a net force acting on it, or
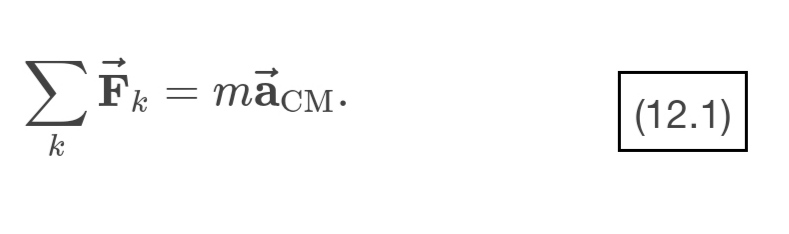
Here, the sum is of all external forces acting on the body, where m is its mass and a⃗ CM is the linear acceleration of its center of mass (a concept we discussed in Linear Momentum and Collisions on linear momentum and collisions). In equilibrium, the linear acceleration is zero. If we set the acceleration to zero in Equation 12.1, we obtain the following equation:

The first equilibrium condition, Equation 12.2, is the equilibrium condition for forces, which we encountered when studying applications of Newton’s laws.

Second Equilibrium Condition
Analogously to Equation 12.1, we can state that the rotational acceleration α⃗ of a rigid body about a fixed axis of rotation is caused by the net torque acting on the body, or
∑kτ⃗ k=Iα⃗ .
(12.4)
Here I is the rotational inertia of the body in rotation about this axis and the summation is over all torques τ⃗ k of external forces in Equation 12.2. In equilibrium, the rotational acceleration is zero. By setting to zero the right-hand side of Equation 12.4, we obtain the second equilibrium condition:

The second equilibrium condition, Equation 12.5, is the equilibrium condition for torques that we encountered when we studied rotational dynamics. It is worth noting that this equation for equilibrium is generally valid for rotational equilibrium about any axis of rotation (fixed or otherwise). Again, this vector equation is equivalent to three scalar equations for the vector components of the net torque:
The second equilibrium condition means that in equilibrium, there is no net external torque to cause rotation about any axis.




