
Rewrite the correct option in your answer sheet.
1. If f(x) = x2 + kx + 1 for all x and f is an even function then the value of K is equal to
(a) 1 (b) 2 (c) 0 (d) -1
2. If A = [-2, 4) and B = (2, 5] then A ∩ B is
(a) [-2, 5] (b) (2, 4) (c) [-2, 2] (d) (-2, 5)
3. If a = √6, b=2, c = √3 - 1 then B is
(a) 45 (b) 30 (c) 60 (d) 135
4. The equation of diameter of the circle x2 + y2 - 6x + 2y = 0, which passes through the origin is
(a) x + 3y = 0 (b) x - 3y = 0 (c) 3x + y = 0 (d) 3x - y = 0
5. The locus is known as parabola if the eccentricity (e) is
(a) equal to 1 (b) less than 1 (c) more than 1 (d) equal to zero
6.  then the projection of b on a is
then the projection of b on a is
(a) 3 (b) 4 (c) 5 (d) 6
7. Form the group of 10 items ∑x = 452, ∑x2 = 24720 and mode = 43.7. Then the coefficient of skewness if
(a) -0.077 (b) 0.077 (c) 0.079 (d) - 0.079
8. The differentiating coefficient of cos-1x + sin-1x is equal to
(a) π/2 (b) 2/√(1-x2) (c) 0 (d) none of these
9. The value of 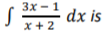
(a) 3x - 7 ln |x+2| + c (b) 3x + 7 ln|x+2| + c (c) 3x - 7 ln|3x-1| + c (d) 3x + 7 ln|3x-1| + c
10. A body is dropped from tower of height 78.4 m. Then the time to reach the ground is
(a) 6s (b) 4s (c) 3s (d) 2s
OR
The demand function P = 12 - 0.5Q then the marginal revenue is
(a) 12-Q (b) 12-PQ (c) 12+Q (d) 12 + PQ
11. . How many iterations do you need to get the approximate root of an equation f(x) = 0 by by bisection method if you start with initial guesses a = 1 , b = 2 and error tolerance 10-4?
(a) 12 (b) 10 (c) 2 (d) 14
"Group B" [ 5 × 8 = 40 ]
12. (a) If p and q are two statements then prove that: p ⇒ q ≡ (~p v q) [3]
(b). Is the function f: N→N defined by f(x) = 3x bijective? [2]
13. (a) Find the square root of the complex number: -5 + 12i. [2]
(b) If ax = by = cz and a, b, c are in G.P. then show that x, y and z are in H.P. [3]
14. (a) In any triangle ABC, prove that [2]
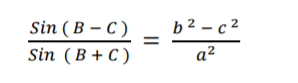
(b) If two pair of straight lines represented x2 - 2axy - 3y2 = 0 and x2 - 2bxy - y2 = 0 are such that each pair bisects the angle between the other pair, prove that ab + 2 = 0. [3]
15. (a) Calculate the Karl Pearson's coefficient of skewness from the following data: [3]
| Profit | below 80 | below 90 | below 100 | below 110 | below 120 |
| No. of cost | 12 | 30 | 65 | 107 | 130 |
b. A class consists of 30 boys and 20 girls. If two students are chosen at random, then find the probability that [2]
i. one is boy another is girl
ii. both are girls
16. a. Evaluate:
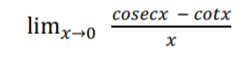
[2]
b. Write the conditions that the graph of the function y = f(x) defined in an interval ( a, b ) is concave upward and concave downward. Find the maximum and minimum values of curve: y = 4x3 - 6x2 - 9x + 1 on the interval (-1,2). Also, find the points of inflection. [3]
17. a. Integrate:

[2]
b. What does an indefinite integral mean? How does it differ from definite integral? Obtain the area bounded by the curves y = 4x and x = 4y. [3]
18. Use simplex method to find the optimal solutions of the LPP:
Maximize: F = 2x + 5y subject to the constraints.

where x,y ≥ 0. [5]
19. a. Resolve a force 30N into two components making angles 30° and 45° with its direction. [2]
b. A stone is dropped into a well reaches the water with velocity 49m/s and sound of striking water is heard in 5⅓ seconds after it is let fall. Find the velocity of the sound. [3]
OR
19. a. If the marginal cost of product is given by C' (x) = 36 - 20x + 6x2, where x is the number of units and initial cost is Rs 20, then find the total cost function and average cost function. [2]
b. The demand function for a good is given as Q = 65 - 5P. Fixed the costs are Rs 30 and each unit produced costs an additional Rs 2. [3]
i. Write the equations for total revenue and total costs interms of Q.
ii. find the break-even points algebraically.
iii. Graph the total revenue and total costs and hence estimate the break-even point.
"Group C" [ 8 × 3 = 24 ]
20. a. Find the domain and the range of the function: [ 4 + 4 = 8 ]
[ 4 + 4 = 8 ]
b. Draw the graph of the function including different characteristics: y = 2Sinx ( 0 ≤ x ≤ 2π )
21. a. Given a = √3 + 1, b = √6, c = √3 -1, solve the triangle ABC. [ 3 + 3 + 2 = 8 ]
b. Show that the angle between the tangents to the parabola y2 = 4x and x2 = 4y at their points of intersection other than origin is tan-1¾.
c. Prove vectorially that: a2 = b2 + c2 - 2bcCosA
22. a. Find from the first principles the derivative of:  [ 4 + 2 + 2 = 8 ]
[ 4 + 2 + 2 = 8 ]
b. A spherical balloon is inflated at the rate of 20cm3/sec. Find the rate of increasing its surface area when the radius is 8cm.
c. Evaluate: 
⁕⁕⁕



 then the projection of b on a is
then the projection of b on a is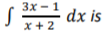
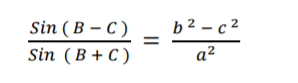
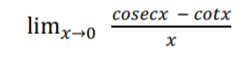 [2]
[2] [ 4 + 4 = 8 ]
[ 4 + 2 + 2 = 8 ]