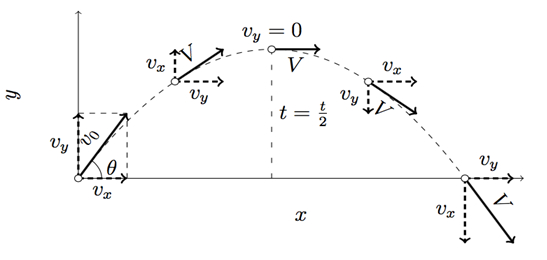
↪ Suppose an object is projected with initial velocity u at an angle θ with the ground which is taken as X-axis.
↪ OY is a vertical line perpendicular to the ground.
↪ The velocity of the object u has two components u_x = uCosθ along X-axis and u_y = uSinθ along Y-axis.
↪ So, initial velocity in horizontal direction is uCosθ and in vertically upward direction uSinθ.

↪ The motion of projectile is two dimensional.
↪ So the horizontal distance is covered by horizontal velocity which is not affected by gravity and vertical distance is due to the vertical velocity which is affected by gravity.

Path of Projectile

↪ Let the object is at point P in time t whose horizontal and vertical distances are x and y. 
↪ As the horizontal velocity is constant, horizontal distance x in the time t is given as

x = uCosθ × t
or, 

↪ Since vertical velocity is affected by gravity, the vertical distance y covered in time t is given as

↪ This is an equation of parabola. Hence the path of a projectile is parabolic.

↪ From above equation,
↪ position of (x, y) of projectile at time t = (uCosθ×t, uSinθ×t - 1/2gt²)

Maximum Height (h_max)

↪ It is the greatest height to which a projectile rises above the point of projection.
↪ At maximum height the vertical velocity of the projectile becomes zero.
↪ From the equation of the motion,

v² = u² + 2gh, we have
0 = (uSinθ)2 + 2(-g)h_max  

or, h_max  

Time of Flight (T)

↪ Time for  which a projectile remains in the air is called time of flight.
↪ As the body projected from the ground and lands on the ground, the vertical displacement is zero.
↪ Therefore from the relation, y = ut + 1/2gt², we have

Horizontal Range (R)

↪ Horizontal distance covered by the projectile during its time of flight is called its range. 
↪ Since there is no acceleration in horizontal direction, so

Maximum Range (R_max)

↪ For a given initial velocity u, horizontal distance depends on angle of projection.
↪ Since Sin2θ has maximum value of 1, the horizontal range will be maximum when Sin2θ = 1

Velocity of Projectile at any instant

↪ If vx and vy are the components of velocity (v) at P in horizontal and vertical directions respectively, then the velocity is given as

↪ If α is the angle made by resultant velocity v with the horizontal, then tanα = v_y/v_x