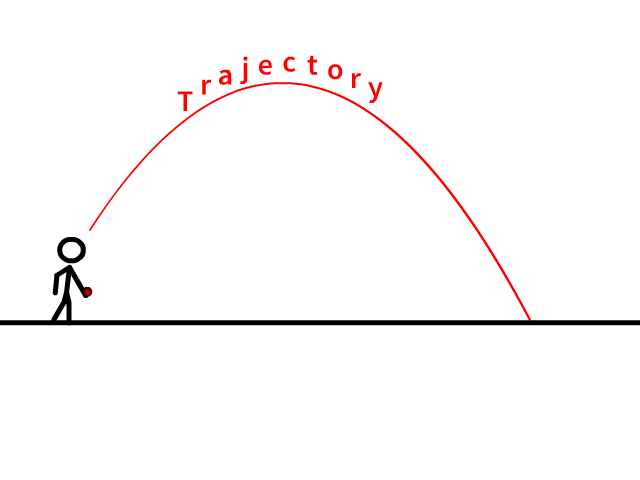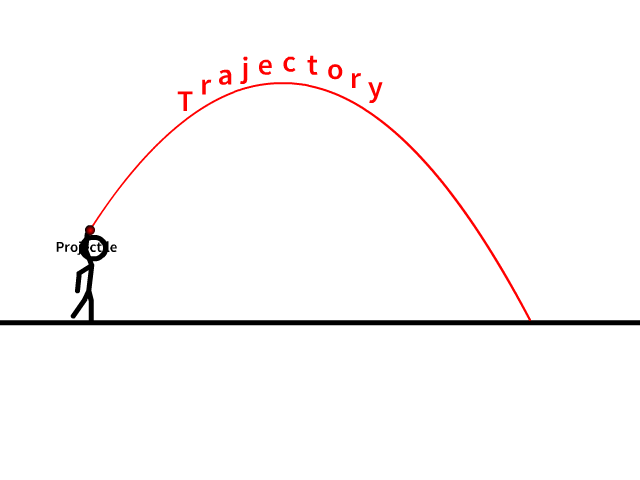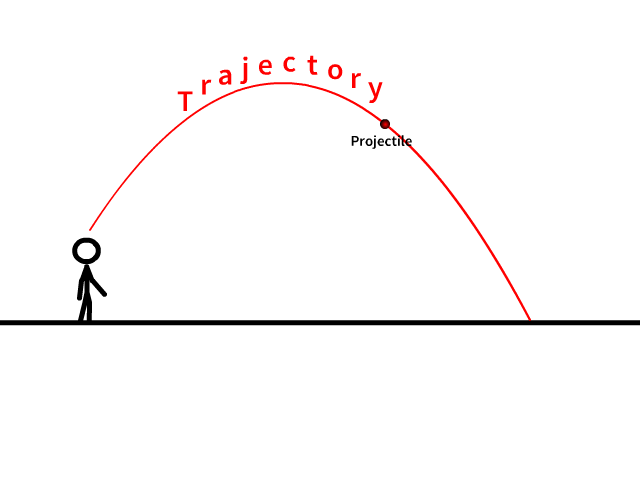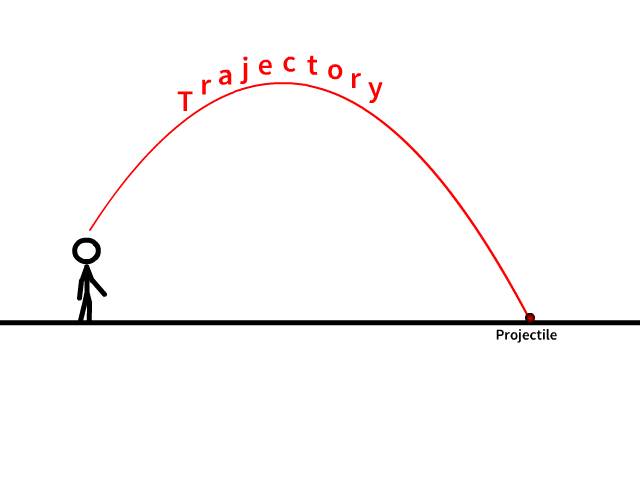
A Projectile 

↪ A projectile is an object which is moving under action of gravity after it has thrown into free space.
↪ For example, an aircraft in its flight is not a projectile because it is driven by its engine but a package dropped from it is indeed a projectile.
↪ Some other examples of projectiles are a bullet fired from a rifle, a shot put or a javelin thrown by an athlete.

↪ The curved or straight path along which a projectile follows in free space is called a trajectory of the projectile.

⁕ Time of flight

↪ It is the time for which a projectile remains in free space after it has fired from the point of projection and reached the point of impact.
↪ It is denoted by T.

⁕ Maximum height

↪ It is the greatest vertical distance to which a projectile rises above the level of the point of projection.

↪ It is generally denoted by H.

⁕ Horizontal range

↪ It is the horizontal distance traveled by a projectile with a uniform velocity in the time of flight between the points of projection and impact.
↪ It is denoted by R.

⁕ The Trajectory of an Object Fired Horizontally 

↪ Let us consider the origin O of a coordinate system as the point of projection, the vertical line OY as the y-axis and the horizontal line OX as the x-axis.
↪ Suppose an object is fired from the point of projection O at a height h above the ground with an initial velocity u horizontally. The point O is like the top of a tower of height h. 

↪ Since the horizontal velocity is perpendicular to the direction of action of gravity, it does not change.
↪ Thus the horizontal distance x traveled by the projectile with the uniform velocity u in time t is

↪ Since the vertical component of the velocity is in the direction of action of gravity, it changes.
↪ Since the initial vertical component, u_y = 0, from 

,the vertical distance traveled by the projectile in time t is

↪ From (2), putting the value of t in (3), we get

↪ This is an equation of a parabola.
↪ Thus the trajectory of the projectile fired from the top of a tower horizontally is a parabola.
↪ Let v be the velocity of the projectile at point P at any time t in the course of its flight. 

↪ Thus the horizontal component of v , v_x = u

and from v = u + at, the vertical component of v ,
v_y = 0 + gt = gt

∴ the magnitude of v is

↪ If β is the angle made by the velocity v with the horizontal, then the direction of v is 

⁕ Time of flight

↪ Putting s = h and t = T in , we get,

↪ This is the time of flight.

↪ From (5), the magnitude of the velocity at the point of impact Q is

↪ From (6), the direction of the velocity at the point of impact Q is

⁕ Horizontal range

↪ The horizontal range

↪ This is the horizontal range.