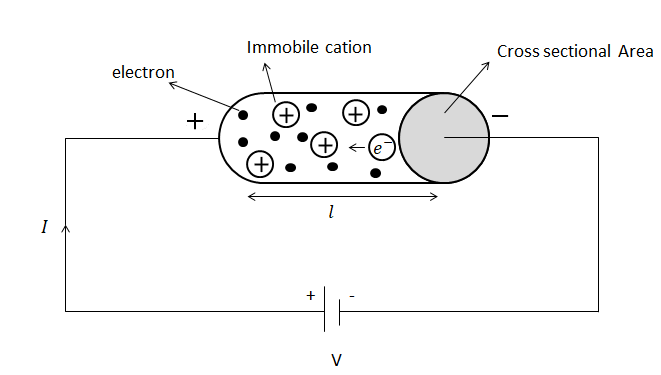
Consider a metallic conductor contains a large number of free electrons which are moving randomly in all directions. Let such electrons are marked as 1,2,...n which are moving with random velocities u₁,u₂,u₃....u_n then taking their average;

u_av =(u₁ + u₂+ ⋯ + u_n)/n= 0.  Thus, there is no net flow of charge in any direction.

Now when the electric field is applied these electrons are accelerated with the acceleration given by

a =eE/m

These electrons move on for time τ₁,τ_2,τ₃,...,τ_{n .}  So the average time spent by each electron before they collide with the atom is given by

τ =(τ₁ + τ₂ + ⋯ + τ_n )/n

This time is called the relaxation time. The relaxation time is the average time spends by the electrons between two successive collisions. In a good conductor like metals, its value is of the order of 10^-14 seconds. The final velocities acquired by these electrons inside the metal in the presence of an electric field is given by,

v1 = u1 + aτ1

v2 = u2 + aτ2

v3 = u3 + aτ3

.

.

.

vn = un + aτn

Thus the average velocity is given by

v_av = 0 + a τ

v_av = (eE)/m x τ

This is the drift velocity of electrons. It may be defined as the average velocity gained by the free electrons of a conductor in the opposite direction of the externally applied electric field.