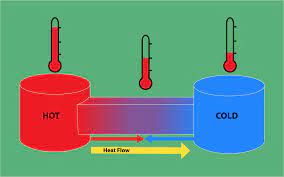
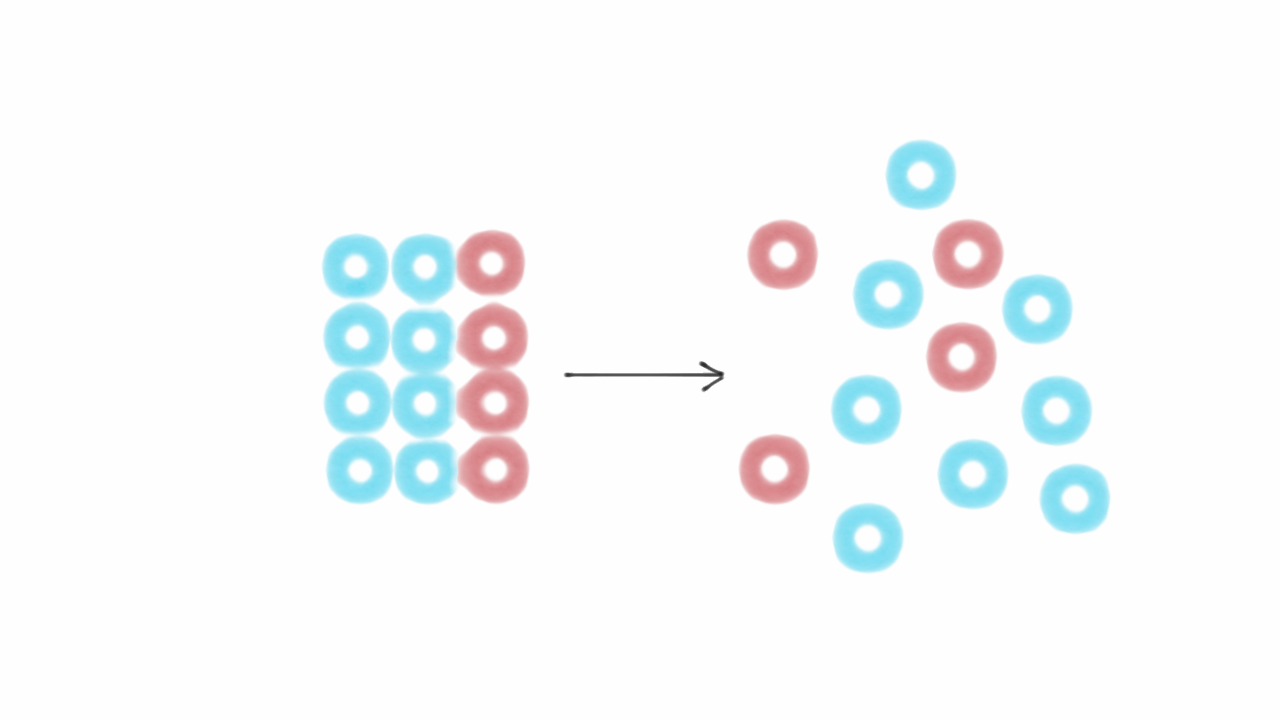
Entropy change for a phase transformation

The phase transformation of a substance is carried out reversibly at constant temperature and fixed pressure generally at one atmosphere.

The entropy change of melting is defined as 

where,  = enthalpy change of melting (fusion).

T_m = melting temperature.

The entropy change of vaporization is defined as 

Where,  = enthalpy of vaporization 

T_b = Boiling temperature

The entropy change q sublimation is defined as 

Where  = enthalpy change of sublimation

T_s = sublimation temperature

Entropy change in chemical reaction

The entropy change of a chemical reaction is defined as their difference between the sum of the entropies of all the products and the sum of entropies of all the reactants. Let us consider a general reaction:

  For this reaction 

Total entropy of product (S product) = (cS_C + dS_D)

Where, c is number of moles of C and d is number of moles of D. S_C and S_D are the entropies of C and D.

Similarly total entropy of reactant (S reactant) = (aS_A +bS_B)

where,

a is no of moles of A

b is no of moles of B

S_A is entropy of A

S_B is entropy of B

Standard entropy:

The entropy of 1 mole of substance in pure state at 1 tm pressure and 25°C temperature is known as standard entropy. It is defined by a symbol S°.

Relation between enthalpy and entropy

Helmholtz – free energy (work function)

The energy which is used for doing useful work at constant volume and constant temperature is known as Helmholtz free energy. It is denoted by a symbol “A”.

Mathematically, it is defined as

A = E - TS ………..(i)

Where, E= initial energy

T = Temperature

S = Entropy

The change in Helmholtz free emerge is denoted by a symbol ‘ΔA’ and ΔA = A₂ – A₁ …………………….(ii)

Where, A₂ = Helmholtz free energy of final state.       

               A₁ = Helmholtz free energy of initial state

Using eqn (i) equation (ii) becomes

We know that

So equation (iii) becomes

ΔA = ΔE – q …………….(iv)

From first law of thermodynamics

Q = ΔE + W

So, ΔA = ΔE – ΔE – W

∴ ΔA = -W

From equation (v) we conclude that d decrease in Helmholtz free energy is equal to the maximum work done by the system.

Gibb's free energy:

Criteria of spontaneity in terms of free energy and entropy

1.      In terms of free energy	2.      In terms of entropy
i.                 If ΔG > 0 i.e ΔG = +ve The process is non spontaneous	i.                 If ΔS> 0 i.e. ΔS= +ve The process is spontaneous
ii.                If ΔG < 0 i.e. ΔG = -ve The process is spontaneous.	ii.                If ΔS < 0 i.e. ΔS = -ve The process is non spontaneous.
iii.               If ΔG = 0 iv.               The system remains in equilibrium.	iii.               If ΔS = 0 The system remains in equilibrium.

Deriving the criteria of spontaneity form Gibbs-Helmholtz equation:

According to Gibbs-Helmholtz equation

          ΔG = ΔH - TΔS

This equation combines in itself both the factors which decide the spontaneity of a process, namely

(a)    The energy factors, ΔH

(b)   The entropy factors, TΔS

(Thus ΔG is the resultant of the energy factor (i.e. tendency for minimum energy) and the entropy factor (i.e. the tendency for maximum randomness)

Depending upon the signs of ΔH and TΔS and their relative magnitudes, the following different possibilities arise:

a.      When both ΔH and TΔS are negative i.e., energy factor favors the process but randomness factor opposite it. (Exothermic process)

i.                 At low temperature, ΔH > TΔS, the process is spontaneous and ΔG is -ve.

ii.                At high temperature, ΔH < TΔS, the process is non spontaneous and ΔG is +ve

iii.               If ΔH = T ΔS, the process is in equilibrium and ΔG is zero.

 

b.      When both ΔH and TΔS are positive i.e, energy factor opposes the process but randomness factor favors it. (Endothermic process)

i.                 At low temperature ΔH > TΔS, the process is non spontaneous and ΔG is positive.

ii.                At high temperature ΔH < TΔS, the process is spontaneous and ΔG is negative.

iii.               If ΔH = TΔS, the process is in equilibrium and ΔG is zero.

 

c.      When ΔH is negative but ΔS is positive i.e., energy factors as well as the randomness factor favour the process will be highly spontaneous and ΔG will be always negative.

d.      When ΔH is positive but ΔS is negative i.e energy factor as well as the randomness factor oppose the process. The process will be highly non spontaneous and ΔG will be always positive. ( Endothermic process)