Dynamics

Before going any further in the topic, I want you to think for a second and find out what is dynamics? You will now be intertwined with the thoughts of what really is dynamics. To be clearer on the topic, let’s roll this way; it might be helpful for you. In the branch of Physics, there are basically factors which we account while the object is in motion; one of them being the dynamics.

The best way of looking this is to visualize a body which is in motion. We might look the motion in two different ways; the one with the focus without considering the cause which produces it or the cause which produces the motion. These two factors are enlisted in the dynamics.

Newton's Laws of Motion

Isaac Newton formulated the three simple laws of motion that can be used to study the object in motion. These are basically known as Newton’s First Second and Third laws of motion.

Newton’s First Law:

This law states that, “Everybody continues to be in the state of its rest or of uniform motion in a straight line, unless acted by an external force to change that state.” This law is the foundational law and also known as law of inertia.

Inertia: It is basically the inability of the body to remain in its state of rest or uniform motion in a straight line.

There are three types of inertia; Inertia of rest, motion and direction.

  1)    Inertia of rest: It is defined as the inability of the body to remain in its state of rest unless acted by and external force. The best example for this is: during the starting of the vehicle, we tend to move backward. It is the because the body’s tendency was to remain in its state of rest so we fall backward.

  2)    Inertia of motion: It is defined as the inability of the body to remain in its state of motion. One of the examples is when you are running really fast and your friend requests you to stop you can’t immediately stop. It is because your body’s tendency is to remain in the motion so we require extra time to come in rest.

  3)    Inertia of direction: It is the inability of the body to change the direction. One example is when you’re inside the bus and bus is about to take round turn you tend to fall outward. This is due to Inertia of direction.

Newton's first law also gives the definition of the force. As it mentioned that body only changes its motion when any external agent acts on them. Hence, the force is any external agent that changes the state of the system.

Newton's Second law of motion:

This law states that, “The rate of change of momentum of a body is directly proportional to the force and changes takes place in the direction of force.” Mathematically;

Here p is the momentum and F is the force applied.

The Newton’s second law gives the measurement of force. This can be shown in the following derivation:

Let us consider a body moving with velocity v₀ and the force F is acted on it then its velocity will change and becomes V_t in time t. Then, from the newton's second law of motion,

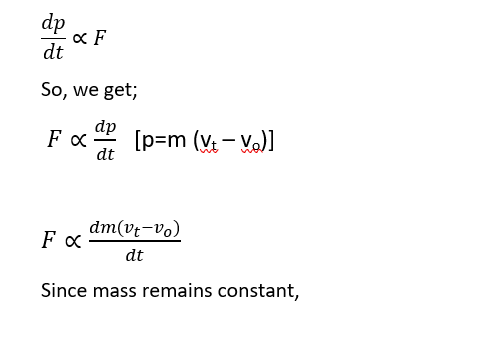
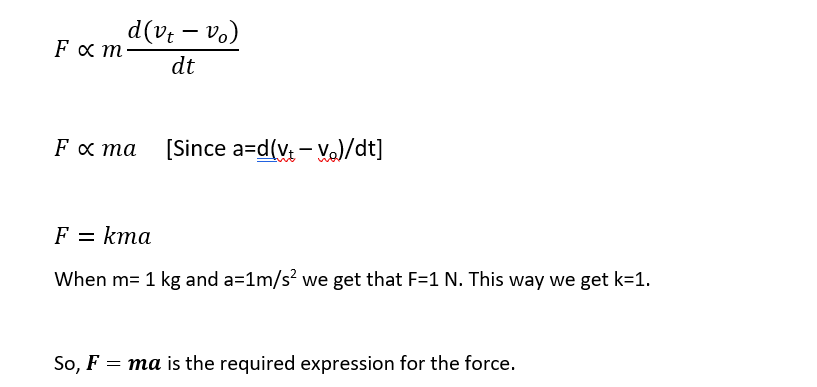
Newton's Third Law of Motion:

This law states that, “To every action there is equal and opposite reaction.”

This statement is quite contradicting as it might mean two equal and opposite force might cancel each other but it is not the case. The best example can be of launching of the rocket. The gases thrown outward from the rocket pushes the air backward as a result upward thrust is generated by the air on the rocket. This way rocket launches off.

Conservation of Linear momentum:

This principle means that, “In an isolated system, the net change in momentum is zero i.e., the initial momentum and the final momentum is equal.”

To prove this, we have following consideration:

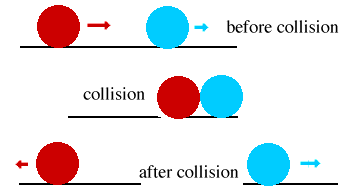
Let us consider two bodies A and B moving with velocities u_A and u_B. Let us assume that the velocity u_B is greater than u_A . After certain time they collide and their momentum changes i.e. velocities become v­_A and v_B . Here following changes happen during time interval t.

This clearly proves that the initial momentum is equal to the final momentum if no external force acts on the system.