An Introduction to Work and Energy
WorkScientifically,Work is said to be done by a force when the force produces a displacement in the body on which it acts in any direction except the direction perpendicular to the direction of th...
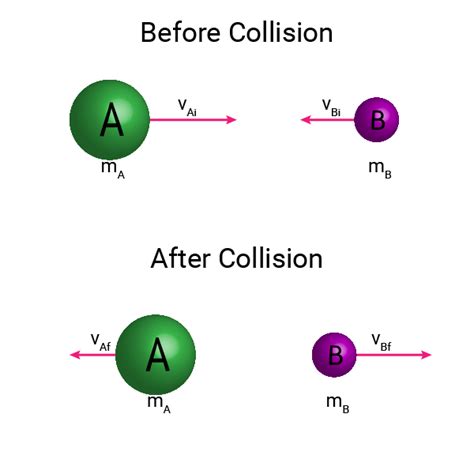
The elastic collision in which the colliding particles moving along the same straight line path before and after the collision is called one-dimensional elastic collision.
Consider two bodies A and B having respective masses m1 and m2 are moving with respective velocities u1 and u2 is straight line such that u1 > u2 before collision as shown in figure . Let, the bodies collide elastically and v1 and v2 be their respective velocities after collision.
Applying law of conservation of linear momentum,
m1u1 + m2u2 = m1v1 +m2v2 ..........(1)
or, m1(u1 – v1) = m2(v2 – u2) ...........(2)
Since in an elastic collision, total kinetic energy also remains conserved. Therefore,


From equation (7) and (8), the velocities of the bodies A and B, after collision can be calculated.
Special cases
· When both the colliding are of the equal masses then, m1 = m2 = m(say)
From(7), v1 = u2
From(8), v2 = u1
This shows that if two bodies having equal masses collide elastically in one-dimension, then they simply interchange their velocities after the collision.
