Capacitors

Capacitors are the devices which are known well for storing charges for different purposes including power conditioning, signal coupling or decoupling, electronic noise filtering, and remote sensing.

Capacitors generally consists of two conducting surface which are separated by certain distance and between the space there is either vacuum or air or any dielectric medium.

Units and Dimensions:

The ability of a capacitor to store charge is said to be capacitance which can be expressed mathematically in the form (C=Q/V) where C,Q and V refers to Capacitance, Charge and voltage respectively.

The unit of Capacitance is Farad(F) but the smaller units of it such as micro-farad and pico-farad are generally used in circuits.

# Capacitance of different Capacitors:

1) Isolated sphere:

    For this we consider an isolated sphere of radius R and having charge Q on its surface.
From definition of Potential,V = Q/(4πε0 R)Q/V = 4πε0 RC = 4πε0 R

Hence The capacitor of an Isolated sphere is equal to quantity 4πε0 R.
In CGS unit, Capacitance of isolated spherical capacitor is numerically equal to the radius since the quantity 4πε0=1.
2) Spherical Capacitance:

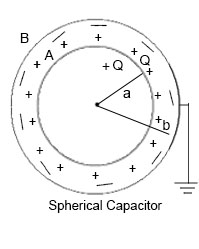
Two concentric spherical conducting shells are separated by vacuum. The inner shell has total charge +Q and outer radius $a^{}$, and outer shell has charge -Q and inner radius $b^{}$. 

Due to the charge on sphere A an equal and opposite charge -q is induced on the surface (inner) is induced in B. Since the B sphere is earthed the +q charge on outer surface travels back to Earth. This way The potential due to sphere A is 

Since potential due to sphere B is zero.

The total potential is given by A. Then,

The Capacitance is given by:

This way, the Capacitance of the spherical capacitance is deduced.

$$ϵ0$$